Overview:
My Approach to Curriculum Writing

by Kirby Urner
First posted: Feb 9, 2001
Last modified: June 28, 2006

Sometime in the not so distant past, math went through a dark age -- literally, in that it was "lights out" for visualizations. Students were supposed to empty their minds of any naive pictures or diagrams and just get used to operating with symbols. This was considered the "in" way to think about matters mathematical -- math, like the rest of culture, is not immune from fads.

Now the pendulum is swinging back to where visualizations are no longer considered naive. Semiotics and Wittgenstein have taught us to see graphical and lexical elements as a part of the same semantic continuum, neither intrinsically more "abstract" than the other. Even "visual proofs" are coming back into vogue.[1]

We also have the "left versus right brain" terminology, which carries weight regardless of whether neuroscience justifies it entirely (actually, there's a lot of evidence for hemispheric specialization).

Traffic between East and West has only increased in this last century (1900s) and the right/left brain talk maps fairly well to yin/yang talk -- there's an isomorphism here, or you can make it work that way. And this concept of balance, of developing both hemispheres, of not letting either atrophy, is having an impact on math education theories, and on pedagogy in general.

So visualizations, the importance of the imagination, is making a come back under the aegis of the right brain's champions.

As a curriculum writer, I too encourage right brain approaches to mathematics. This hemisphere I associate not just with visual/spatial/imaginative abilities, but with the concept of cardinality (vs. ordinality) -- a link I learned about from Midhat Gazale.[2]

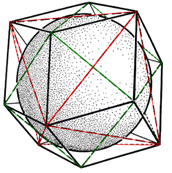
On the spatial front, I encourage a kind of "mental geometry" to develop alongside "mental arithmetic", and do so by exploiting the ancient tradition of nesting polyhedra to form a "maze" or "matrix". It's something the sacred geometers were into, down through the theosophists in our own time.

Given this history, our graphics and visuals may tend to raise some eyebrows.[3] But that's OK. I think it's more interesting to students as well, to connect to these arts and traditions, while developing their right brain abilities to consider geometry in the mind's eye. Opportunities to bring up historical topics, which offer insight into how we came to be who we are, should not be ignored.

Where I part company from most polyhedron nesters is I'm not so fixated on the Platonic Five, thanks to my being a long time student of the Fuller syllabus, i.e. a reader of books by the late R. Buckminster Fuller. Rather than the pentagonal dodecahedron, Bucky, like Kepler, was more into the rhombic dodecahedron, because the latter is defined by a sphere packing known variously as the CCP or FCC (or IVM if you're reading Fuller's Synergetics -- the octet truss in architecture).

The rhombic dodeca isn't even an Archimedean, let alone a Platonic, and yet chemistry really is a lot about lattices, which may be referenced to packed spheres. The CCP, like the XYZ coordinate system, provides a scaffolding, lines of reference, a grid. It should be taught, starting early.

We need geoboards of both varieties: square-based and hexa-based in flatland, and cube-based and dodeca-based in space. The XYZ lattice corresponds to another way of packing spheres by the way (less dense): the SCP (simple cubic packing).

So yes, I'm into sphere packing and push it as a topic accessible even to the very young -- that's made very obvious at my website. And another thing I learned from Bucky: there's a very streamlined and compact way of both nesting and scaling a set of inter-related polyhedra so that not only do they synch with the CCP (with rhombic dodeca = unit radius sphere domain), but they have whole number volumes to boot.

I find this intro to spatial geometry far less off-putting to kids, than the way we phase in non-cubes today. Today, only cubes get to have simple, whole number volumes, while just about everything else is irrationally volumed, unless assembled from cubes, i.e. unless rectilinear, all parallel lines.

Our cubism alienates the other polys, relegates them to the back of the book, to obscurity. Yet this really basic stuff should not be rendered esoteric. It's our obsession with the cube that makes it so. That was Bucky's critique of our whole culture and I think there's enough truth in it that I'm inclined to take decades of practically no discussion of the issue as more evidence that these valuable diagnostic insights have been willfully suppressed by those who should know better than to stand in the way of evolution, yet cling, out of fear and ignorance, to the status quo.

Here's the new volumes chart: [4]

        
  Shape                   Volume
  ===============================
  Tetrahedron                  1
  Cube                         3
  Octahedron                   4
  Rhombic Dodeca               6
  Cubocta                     20

Now, how does this work? First of all, we're nesting polyhedra, ala the ancient tradition of doing so, going back to Pythagoras and before. We're organizing them concentrically (they all share the same center). The tetrahedron comprises the face diagonals of the cube. Another tetrahedron, crossing the edges of the first at 90 degrees, defines the other 4 of the cube's 8 corners.

These two intersecting tetrahedra are what Kepler and others called the stella octangula. You can also see it as an octahedron with tetrahedral tips (a stellate), these 8 tips defining the corners of our cube. So we call it a "duo-tet" cube -- because formed from these two interpenetrating tetrahedra (I use an orange and black duo-tet as the logo of my company by the way -- 4D Solutions, named to emphasize continuity with Fuller's own use of 4D as a kind of logo).[5]

I mentioned an octahedron, defined by the intersection of the two tetrahedra (you could use intersection notation at this point). That octahedron has edges ½ those of the tetrahedron, and therefore 1/8^th the volume of an octahedron with edges the same as the tetrahedron's.

Double the edges, and volume goes up by 8 -- it's in the California standard: 7^th graders should all know about the edges:surface area:volume relationship, an exponential or powering relationship with exponents 1:2:3.

I won't go into all the geometric dissections and rearrangements of pieces (modules, parts), and just say that a series of wordless geometry cartoons easily communicates volumes about volume. The students will see, by means of "visual proofs", that the octahedron has a volume of 4, and inscribes as the long diagonals of the rhombic dodeca's 12 faces, while the cube's edges inscribe as the short diagonals. It's a very tight arrangement then:

tetra + dual tetra = cube
  cube + dual octa = rhombic dodeca  
                   = domain of unit radius sphere
				   

And 12 such spheres tightly packed around a nuclear sphere, CCP style, form the vertices of a cuboctahedron of volume 20.

From here, you can keep packing outward, layer after layer of spheres, always cuboctahedrally conformed, with 10 L² + 2 spheres in each layer (L = layer number, starting with 12 when L=1).

There's a way to use simultaneous equations, matrix algebra, or even Bernoulli numbers, to derive a formula for the cumulative number of spheres in all layers (plus nuclear). Let's share that!

So that's what I mean by "mental geometry". There's more to it of course, but this is the basic framework of what's developed as a kind of "home base" for the mind's eye. Clearly the tetrahedron is prominent. This is a divergence from the cubist standard, but is convergent with other trends and schools of thought i.e. it may be unfamiliar, but it's certainly not out of the ballpark, in the sense that tetrahedra are intrinsic to geometry.

Tetrahedra are the simplest volumes after all, if limiting entrants to shapes made from edges, vertices and faces (the sphere being a limiting shape, a very high frequency polyhedron of some kind e.g. an icosasphere). The tetrahedron has only 6 edges whereas the cube uses 12. In this sense, the tetrahedron, or simplex, is the most primitive enclosure. That needs to be stated directly, in no uncertain terms. If it's not part of the California standard, it really should be.

So how do we connect to "mental arithmetic" then? Now that I've outlined the right brain's regimen (including mental exercises), where do we connect to the other hemisphere? Answer: through figurate numbers and Pascal's Triangle.

Figurate numbers may be envisioned as sphere packings. The triangular numbers look like something you'd see in a Pool Hall -- Pool Hall math. The square and cube-shaped numbers suggest XY, or the SCP/XYZ lattice. So we're starting to talk about number series, as the triangular numbers are likewise the sums of consecutive positive integers. Lots of relationships might be developed as the students consider and explore, plus we include a derivation of the aforementioned 10 L² + 2, which applies to icosahedral shells, not just cuboctahedral (links to viruses, buckyballs, geodesic spheres).

And with Pascal's Triangle, we've got links to the Binomial Theorem (factorials, permutations, combinations, probability, Bell Curve), Fibonacci Numbers, Bernoulli Numbers, Triangular and Tetrahedral Numbers.

That's a very rich set of concepts to go forward with. Fibonaccis connect to phi, Bernoullis to sums of the form:

where c = integer > 0

or, when c < 0, to Euler's zeta function -- Riemann's if complex.

Throw in continued fractions, primes vs. composites, and some modulo arithmetic, and you've set the stage with a lot of important and inter-related concepts (gcd, lcm, fractions, Fermat's little theorem, cyphers...) Plus phi gets you back to geometry, to five-fold symmetry, and to the so-far missing Platonics (the pentagonal dodecahedron and its dual, the icosahedron). We also have Pascal's Tetrahedron, and the trinomial theorem, if we like.[6]

Functions and relations, polynomials, trig, vectors, and much of what's conventionally covered in math class (plus more that isn't), all have easy segues or hyperlinks from this core network of key concepts. We don't lose content, and we gain a more tightly integrated curriculum, with left and right brain faculties co-functioning in far greater harmony, producing more powerful synergies. Sure, that's hype, more pro-OCN propaganda, but there's plenty of substance to back it up.

The left brain stuff gets developed in tandem with computer programming (not just calculators), and the right brain stuff gets developed in tandem with computer graphics -- driven behind the scenes by the computer programs. Left brain numeric methods result in right brain artistic renderings. We've got the bridge between math and art. All we need now is to phase in music (something computers are good for as well). That's something I haven't gone into much yet, but some of my colleagues are exploring in that direction.[7]

1. James Robert Brown. Philosophy of Mathematics: an introduction to the world of proofs and pictures (London: Routledge, 1999)
2. Re: Cardinality vs Ordinality
3. see L. Gordon Plummer. The Mathematics of the Cosmic Mind (Wheaton IL: Theosophical Publishing House, 1970) -- a book both Kiyoshi and I agreed contains a lot of racist elements, but I'm mentioning it here for the "maze" depictions
4. More re volumes
5. 4D Solutions, Portland (PDX)
6. Getting Serious About Series (Numeracy + Computer Literacy essay)
7. See Jay Kappraff. Connections: the geometric bridge between art and science. (New York: McGraw-Hill, 1991). For more music links. Sir Roger Penrose had an interesting approach to music using a circle, which he shared with us at the 1997 Oregon Math Summit

For further reading:

• A Short Talk on Geometry: Part I, Part 2 (math-learn, May 11, 2001)
• Geometry Lab: Part 1, Part 2 (math-learn, May 12-13, 2001)
• Which Polynomial? (math-teach, July 30, 2005)
• This ain't your parent's math (math-learn, Dec 02, 2005)

The first draft of this essay was originally posted to math-learn on Feb 4, 2001

Oregon Curriculum Network