"""
stickworks.py

Some infrastructure for working with Vectors and Edges, including
an xyplotter generator and axes maker.

By Kirby Urner, Sept 13, 2006

Updated Sept 29, 2006:
make Edge color a class-level attribute
add funky derivative demo
refactor a bit

Updated for Martian Math, 2010
Brought over Qvector subclass from coords.py

Code:
http://www.4dsolutions.net/ocn/python/stickworks.py

For colorized source:
http://www.4dsolutions.net/cgi-bin/py2html.cgi?script=/ocn/python/stickworks.py

Some relevant discussion:
http://mail.python.org/pipermail/edu-sig/2006-September/007145.html
http://mail.python.org/pipermail/edu-sig/2006-September/007149.html
http://mail.python.org/pipermail/edu-sig/2006-September/007150.html
http://mail.python.org/pipermail/edu-sig/2006-September/007312.html
"""

from visual import vector, cylinder, cross, dot, diff_angle, color
import visual
from operator import add, sub, mul, neg

root2   = 2.0**0.5

class Vector (object):

    """
    A wrapper for visual.vector that expresses a cylinder via draw(),
    always pegged to the origin
    """

    radius = 0.03
    
    def __init__(self, xyz, color=(0,0,1)):
        self.v = vector(*xyz)
        self.xyz = xyz
        self.color = color
        self.cyl = None

    def draw(self):
        """define and render the cylinder"""        
        self.cyl = cylinder(pos = (0,0,0), axis = self.v, radius = self.radius, color = self.color)

    def erase(self):
        """toss the cylinder"""        
        if self.cyl:
            self.cyl.visible = 0
        self.cyl = None

    def __repr__(self):
        return 'Vector @ (%s,%s,%s)' % self.xyz

    # some vector ops, including scalar multiplication
    
    def diff_angle(self, other):
        return self.v.diff_angle(other.v)

    def cross(self, other):
        temp = cross(self.v, other.v)
        return Vector((temp.x, temp.y, temp.z))
    
    def dot(self, other):
        return dot(self.v, other.v)

    def __sub__(self, other):
        temp = self.v - other.v
        return Vector((temp.x, temp.y, temp.z))

    def __add__(self, other):
        temp = self.v + other.v
        return Vector((temp.x, temp.y, temp.z))

    def __mul__(self, scalar):
        temp = self.v * scalar
        return Vector((temp.x, temp.y, temp.z))

    __rmul__ = __mul__

    def __neg__(self):
        return Vector((-self.v.x, -self.v.y, -self.v.z))

    def _length(self):
        return pow(self.v.x ** 2 + self.v.y ** 2 + self.v.z ** 2, 0.5)

    length = property(_length)

    def spherical(self):
        """Return (r,phi,theta) spherical coords based on current (x,y,z)"""
        r = self.length()

        if self.xyz[0]==0:
            if   self.xyz[1]==0: theta =   0.0
            elif self.xyz[1]< 0: theta = 270.0
            else:                theta =  90.0
            
        else:            
            theta = math.atan(self.xyz[1]/self.xyz[0]) * rad2deg
            if   self.xyz[0]<0 and self.xyz[1]==0:  theta =    180
            elif self.xyz[0]<0:                     theta =    180 + theta
            elif self.xyz[0]>0 and self.xyz[1]<0:   theta =    360 + theta

        if r==0: phi=0.0
        else: phi = math.acos(self.xyz[2]/r) * rad2deg
        
        return (r,phi,theta)

    def quadray(self):
        """return (a,b,c,d) quadray based on current (x,y,z)"""
        x=self.xyz[0]
        y=self.xyz[1]
        z=self.xyz[2]
        a = (2./root2) * ((x>=0)*x   + (y>=0)*y   + (z>=0)*z)
        b = (2./root2) * ((x<0)*(-x) + (y<0)*(-y) + (z>=0)*z)
        c = (2./root2) * ((x<0)*(-x) + (y>=0)*y   + (z<0)*(-z))
        d = (2./root2) * ((x>=0)*x   + (y<0)*(-y) + (z<0)*(-z))
        return self.norm((a,b,c,d))

    def norm(self,plist):
        """Normalize such that 4-tuple all non-negative members."""
        return tuple(map(sub,plist,[min(plist)]*4)) 
    
    def norm0(self):
        """Normalize such that sum of 4-tuple members = 0"""
        q = self.quadray()
        return tuple(map(sub,q,[reduce(add,q)/4.0]*4))
    
class Qray(Vector):
    """Subclass of Vector that takes quadray coordinate args"""
    
    def __init__(self, arg, color=(0,0,1),*flag):
        """Initialize a vector at an (a,b,c,d) tuple (= arg).
        
        NOTE: in accompanying essay, xyz units = sphere diameter
        i.e. Vector((1,0,0)).length() is 1 D, therefore quadray
        inputs must be scaled by 1/2 to fit this context, i.e.
        tetra edge defined by 2 basis quadrays = 1 D."""

        if len(arg)==3:  arg = Vector(arg).quadray() # if 3-tuple passed
            
        self.coords = self.norm(arg)

        a,b,c,d     =  self.coords
        self.xyz    = ((0.5/root2) * (a - b - c + d),
                       (0.5/root2) * (a - b + c - d),
                       (0.5/root2) * (a + b - c - d))
        self.v = vector(self.xyz)
        self.color = color
        self.cyl = None

    def __repr__(self):
        return "Qvector " + str(self.coords)
                    
    def dot(self,v1):
        """Return the dot product of self with another vector.

        return a scalar"""
        scalar = 0
        return 0.5*reduce(add,map(mul,self.norm0(),v1.norm0()))

    def cross(self,v1):
        """Return the cross product of self with another vector.
        return a Qvector"""
        
        A=Qray((1,0,0,0))
        B=Qray((0,1,0,0))
        C=Qray((0,0,1,0))
        D=Qray((0,0,0,1))
        a1,b1,c1,d1 = v1.quadray()
        a2,b2,c2,d2 = self.quadray()
        k= (2.0**0.5)/4.0
        thesum =   (A*c1*d2 - A*d1*c2 - A*b1*d2 + A*b1*c2
               + A*b2*d1 - A*b2*c1 - B*c1*d2 + B*d1*c2 
               + b1*C*d2 - b1*D*c2 - b2*C*d1 + b2*D*c1 
               + a1*B*d2 - a1*B*c2 - a1*C*d2 + a1*D*c2
               + a1*b2*C - a1*b2*D - a2*B*d1 + a2*B*c1 
               + a2*C*d1 - a2*D*c1 - a2*b1*C + a2*b1*D)
        return k*thesum
    
    def quadray(self):
        return self.coords
    
class Edge (object):

    """
    Edges are defined by two Vectors (above) and express as cylinder via draw().
    """

    radius = 0.03
    color = (1,0,0)

    def __init__(self, v0, v1, color=None):
        if not color==None:
            self.color = color
        self.v0 = v0
        self.v1 = v1
        self.cyl = None        

    def draw(self):
        """define and render the cylinder"""
        temp = (self.v1 - self.v0).xyz
        self.cyl = cylinder(pos = self.v0.xyz, axis = vector(*temp), 
                              radius = self.radius, color = self.color)

    def erase(self):
        """toss the cylinder"""
        if self.cyl:
            self.cyl.visible = 0
        self.cyl = None
        
    def __repr__(self):
        return 'Edge from %s to %s' % (self.v0, self.v1)


def getedges(faces):
        """
        Extract edges from the faces list.
        """ 
        edges = set()
        for f in faces:
            pairs = zip(f , f[1:]+(f[0],))
            for p in pairs:
                edges.add(tuple(sorted(p)))
        return list(edges)                

def xyplotter(domain, f):
    """
    domain should be an initialized generator, ready for next() triggering.
    f is any function of x.  Consecutive Vectors trace connected edges.
    """
    x0 = domain.next()    
    y0  = f(x0)        
    while True:
        x1 = domain.next()
        y1 =  f(x1)
        e = Edge( Vector((x0, y0, 0)), Vector((x1, y1, 0)) )
        e.draw()
        yield None
        x0, y0 = x1, y1
        
def axes(x=0,y=0,z=0):
    """
    Draw some axes on the VPython canvas
    """
    v0 = Vector((x,0,0))
    v0.draw()
    v0 = Vector((-x,0,0))
    v0.draw()

    v0 = Vector((0,y,0))
    v0.draw()
    v0 = Vector((0,-y,0))
    v0.draw()

    v0 = Vector((0,0,z))
    v0.draw()
    v0 = Vector((0,0,-z))
    v0.draw()

    
def dgen(start, step):
    """
    generic domain generator
    """
    while True:
       yield start
       start += step

       
def testme():
    """
    >>> from stickworks import testme
    Visual 2005-01-08
    >>> testme()

    See:
    http://www.4dsolutions.net/ocn/graphics/cosines.png
    """
    
    from math import cos

    def f(x):  return cos(x)

    d = dgen(-5, 0.1)
    axes(-5,1,0)
    graph = xyplotter(d, f)

    for i in xrange(100):
        graph.next()

def testmemore():
    """
    See:
    http://www.4dsolutions.net/ocn/graphics/pycalculus.png
    """

    def snakeywakey(x):
        """
        Polynomial with x-axis crossings at 3,2,-3,-7, with scaler
        to keep y-values under control (from a plotting point of view)
        """
        return 0.01 * (x-3)*(x-2)*(x+3)*(x+7)

    def deriv(f, h=1e-5):
        """
        Generic df(x)/dx approximator (discrete h)
        """
        def funk(x):
            return (f(x+h)-f(x))/h
        return funk
    

    d1 = dgen(-8, 0.1)
    d2 = dgen(-8, 0.1)
    d3 = dgen(-8, 0.1)
    
    axes(-8,5,3)

    deriv_snakeywakey = deriv(snakeywakey)
    second_deriv = deriv(deriv_snakeywakey)
    
    graph1 = xyplotter(d1, snakeywakey)
    graph2 = xyplotter(d2, deriv_snakeywakey)
    graph3 = xyplotter(d3, second_deriv)    

    Edge.color = (1,0,0)  # make snakeywakey red
    
    for i in xrange(130):
        graph1.next()

    Edge.color = (0,1,0)  # make derivative green
    
    for i in xrange(130):
        graph2.next()

    Edge.color = (0,1,1)  # make 2nd derivative cyan

    for i in xrange(130):
        graph3.next()

if __name__ == '__main__':
    # testme()
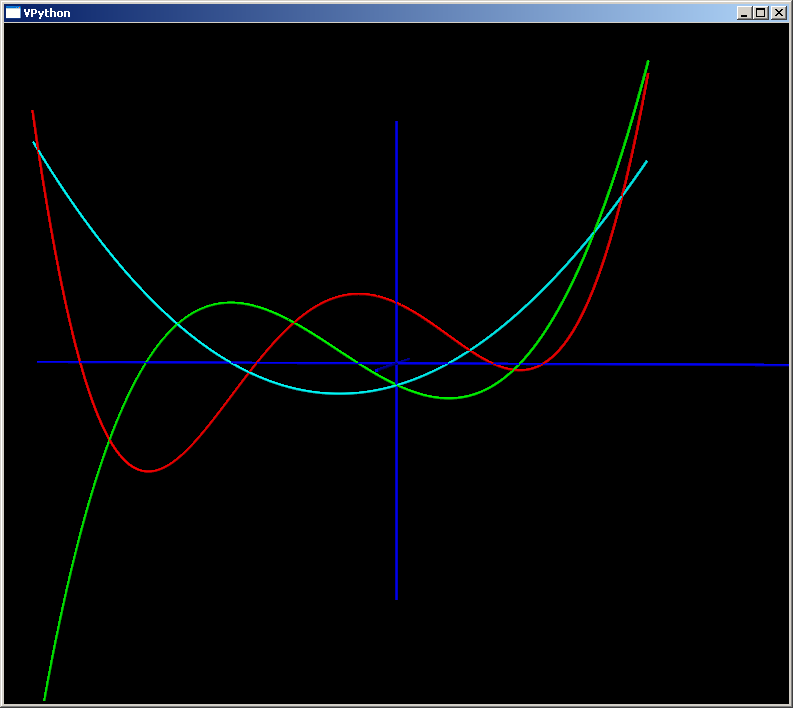
    testmemore()