Serving HexaPents

First posted: July 23, 2006
Last Modified: August 30, 2006

Fig: 1: A Class III Hexapent from Packinon

(click here for OFF file)

geodesic -c 2,3 2 | pol_recip | off_util -O | off2pov > hexapent.pov

Have you ever considered a web site as an actual web? Think of it: a graph of hyperlinks interconnects nodes, web pages, into some shape. The shape is topological, a wiring diagram, more than a rigid solid, but there's a concrete sense of "who the neighbors are": whatever nodes are reachable just one click away.

We may design our web wirings to be as polyhedral as we like, i.e. we could do a "cube" of 8 web pages, each linked to three neighbors in a particular way. Or a tetrahedral site would only have the 4 pages, interlinked by six hyperlinks (or twelve, counting once in each direction).

Or, instead of thinking of corners as web pages, we might instead think of faces. This switch from corners to faces is also a switch to the corners of a paired "dual" polyhedron.

You get a poly's dual when you exchange its faces for corners, corners for faces. The edge count remains constant.

For example, the dual of the cube is an octahedron, while the dual of the cuboctahedron is the rhombic dodecahedron. The tetrahedron is self-dual.

Finding the dual is the purpose of Adrian's pol_recip in the above pipeline (Fig 1), which begins with a Class III omnitriangulated geodesic sphere (which is not the only way to begin, to get a hexapent).

Based on this "web page = face" metaphor, the "nearest neighbors" would be the faces just over the fence, i.e. just across an edge from our present location. On a hexapent, all our faces are hexagons or pentagons, so every cell has six or five neighbors.

Imagine a web server that keeps track of your position on the hexapent, plus those of many others. When you hop to a neighboring cell, the server does a lookup, and, depending on which edge you crossed, serves up that next face -- as a web page.

As you the user hop from cell to cell, you hit web page after web page. These get served up dynamically, on the fly, meaning the server writes the HTML on demand, right when you need to browse it.

Fig. 2: a composite rendering generated from
Bono's dome.exe + a web tutorial on how to texture a ball
with an earth map using POV-Ray

In the Python modules linked below, we go as far as setting up a basic soccer ball of 20 hexagons and 12 pentagons. The higher frequency hexapents will have the same number of pentagons, but maybe a lot more hexagons. They'll perhaps come as left and right handed pairs (or footed, if they're shoes).

The scripts run without fanfare to produce boring ASCII representations of each facet, however the dynamic substitution of self.address and self.neighbors going on will suggest what you might try in on-the-fly HTML, perhaps served in a private testbed setting (where Python's own CGIHTTPServer would be up to the job).

You may also play games with cellular automata using the hexapent. Think up some rules for some Game of Life 2 on this cellular surface. How would you implement it graphically? Could you also spread it out flat, and let the computer keep track of how it all sews up?

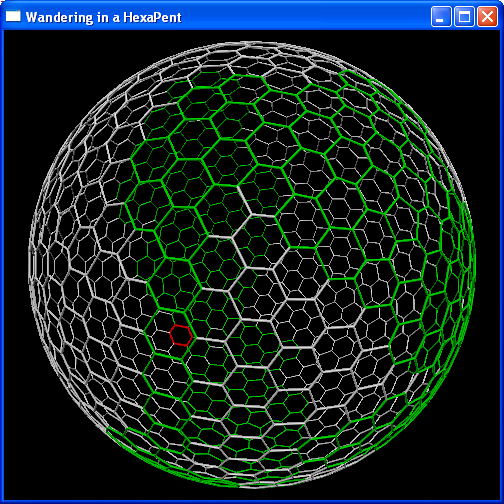
Fig 3: Wandering the HexaPent in VPython

You'll need: gm2.py, gmwanderer.py and the OFF file linked above.

The above VPython window depicts the same polyhedron as in Figure 1, this time with a randomly walking red patch leaving a trail of green. You'll see in gmwanderer.py that I'm using a Cell object to capture info about the currently occupied cell and its 5 or 6 neighbors. Cell's next() method randomly spits back a next neighbor to visit, a process that's repeated for however many cycles.

For further reading:

Return to CP4E
oregon.gif - 8.3 K
 Oregon Curriculum Network