Using Polyhedra to Teach OOP
and Coordinate Geometry Concepts

Chapter 6:
Starting Over in Java

by Kirby Urner
First posted: March 22, 1999
Last modified: March 23, 1999

Lest I delude myself into thinking a current "4D Solution" is the only and/or best, I devote this chapter to a revised Polys package, adopting a host of different strategies, but again using Java. In the next chapter, I repeat this exercise, but this time in an entirely different very high level language (VHLL), Python.

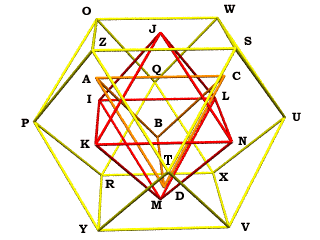
For example, in other contexts I've found it useful to name vertices A-Z and perform vector addition using these letters.

So my new approach employs dictionaries (Hashtable class) to store vertices, edges and faces by name, not simply by numeric array index. This means I can summon the vertices I need by label. Plus I can more easily define my polyhedras' faces using named vertices:

  fdict = new Hashtable(4);
  addfaces(new String[]{"ABC","ABD","ACD","BCD"});

becomes my new syntax of choice, for specifying faces as Strings of vertices (so far I haven't been consistent about going around in a clockwise or counterclockwise fashion, when viewing from outside the shape -- something I might get around to eventually).

Another revision: my Polys class has swallowed Vertex, Edge and Face as internal classes -- useful for giving them shared access to environmental variables, such as the PrintWriter object (required for outputting to file). Each of these embedded classes knows how to "write itself" as a Povray expression: vertices as spheres, edges as cylinders, and faces as polygons. From the Vertex (internal to Polys) class:

  public void writeVert(){
     // write vertex as sphere{} in povray format
     if ( showvert ){
         output.println
         ("sphere{ <"+xyz[0]+", "+xyz[1]+", "+xyz[2]+">," +
           vertdiam + " pigment {color " + vertcolor + "} no_shadow}");
           tickoff = true;
     }
  }

A lot of conversion goes on between Character and String types as I traverse a Hashtable and pick out individual letters for use as keys to another Hashtable e.g. when I parse flist (a passed parameter) to pick out labels for fdict (a shape's faces dictionary):

 // store faces specific to poly in fdict (constructor)
 protected void addfaces(String[] flist){
   String face;
   String[] vertlist;
   for (int i=0;i<flist.length;i++){
        face = flist[i];
        vertlist = new String[face.length()];
        for (int j=0;j<face.length();j++)
        {
            vertlist[j]=new Character(face.charAt(j)).toString();
        }
         addface(flist[i],vertlist);
    }
 }

 private void addface(String ckey, String[] vertlist){
   fdict.put(ckey,new Face(vertlist));
 }

Each subclassed poly starts with full knowledge of 26 labeled vertices, A-Z (defined in the Polys constructor), but transfers only some of them to its personalized vdict vertices dictionary. In other words, pdict (all 26 vertices) is a master lookup table and static variable common to all polys. Because it's static, pdict takes up only one space in memory, common to all polys, whereas each poly also has its personalized set of vertices, edges and faces for individualized transformations (rotations, scaling, translations). The Polys class itself is abstract, meaning it never gets instantiated directly -- yet this class contains most of the intelligence which all its child polys (e.g. Tetrahedron, Octahedron, Cuboctahedron) inherit.

As of this writing, I haven't ported over the Mesh object, nor VRML output capability. This is a more limited implementation so far -- which just as well, as its primary purpose is pedagogical (to teach OOP using polyhedra), not to be exhaustively redundant. I do like the more streamlined structure in this version, plus I can boast that it does do "solids" -- all faces may be filled in and/or selectively enabled.

Also, just to be different, I've implemented rotation by recycling the Quaternion class I defined for another project. As of this writing, I haven't implemented translation or scaling (very easy to do) -- you might want to check back for a later version date on the source code or, even better, implement these features yourself.

My purpose in this final chapter was mostly to remind readers, including myself, to keep an open mind when it comes to programming. Sophisticated programming languages such as Java (one of many) offer enough flexibility to suggest many alternative approaches, each with their own positive and negative attributes.

On-line Resources:

• Chapters I, 2, 3, 4, 5 and 7 of this webtext
• Polys2.zip (source code only). Last modified: March 22,1999
• Some background posts leading up to this version: [ 1][2][3]
• OOP Meets Algebra (Quaternions in Java)

Return to Symbols and Operators

Oregon Curriculum Network