Using Polyhedra to Teach OOP
and Coordinate Geometry Concepts
Chapter 7:
Playing with Python
by Kirby Urner
First posted: August 28, 1999
Last modified: September 1, 1999
In a lot of ways, Python brings us full circle, as many of the features which make it an ideal teaching language were appealing aspects of Xbase (VFP) as well: command line environment, no need to declare variable types, strong objects model. Finally, unlike Microsoft Visual FoxPro, Python is a free language, and cross-platform to boot.
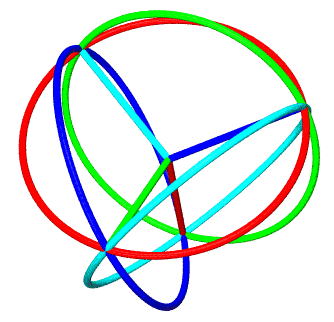
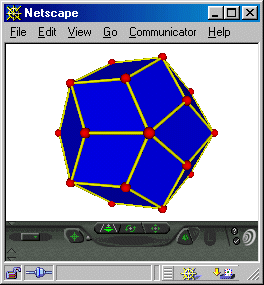
I'm repeating the graphic at right because Python proves very well suited to this "points dictionary" approach to defining various polyhedra as subclasses which share A-Z in common.
In the Java implementation, I used a Hashtable class to store vertices, edges and faces by name. Python makes this even easier by:
- having a built-in "dictionary" type, with easy syntax for storing (name, object) pairs and
- incorporating such a dictionary into the definition of every class, to internally collect its variables and methods.
fdict = new Hashtable(4);
addfaces(new String[]{"ABC","ABD","ACD","BCD"});
In Python I simply write (in my definition of the subclass for a Tetrahedron):
faces = (('A','B','C'),('A','B','D'),('A','C','D'),('B','C','D'))
where the points A,B,C and D have already been defined as part of the superclass data dictionary.
The points A-Z are defined using of a new Vector class which incorporates another attractive feature in Python, not available in either the current Java or VFP: operator overloading. By writing methods for the predefined function names __mul__, __add__, __neg__ and a few others, we can change the behavior of such primitive operators as *,+, - with regard to objects (e.g. vectors and polyhedra). This means we can perform vector addition very straightfowardly in code, once the function definition for vector addition has been made a part of our Vector objects:
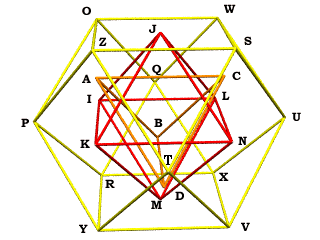
#A-Z form the basic "vocabulary" of needed vertices. The Rhtriac #subclass jitterbugs O-Z to support derivative points a-t (lowercase) #(Icosa and Pdodeca are both subclasses of Rhtriac) A=Vector(quad=(1,0,0,0)); B=Vector(quad=(0,1,0,0)) C=Vector(quad=(0,0,1,0)); D=Vector(quad=(0,0,0,1)) E=-A; F=-B; G=-C; H=-D I=A+B; J=A+C; K=A+D; L=B+C; M=B+D; N=C+D O=I+J; P=I+K; Q=I+L; R=I+M; S=N+J; T=N+K U=N+L; V=N+M; W=J+L; X=L+M; Y=M+K; Z=K+J
Here's our definition of the class method for vector addition, which returns a new vector as output:
def __add__(self,pVector):
# add parameter quadray to self, return new quadray
if type(pVector)==type(self):
outlist = []
for i in range(4): outlist.append(self.data[i]+pVector.data[i])
else: outlist = self.data
return Vector(quad=outlist)
Once A-Z have been defined in the Poly class -- by setting A-D equal to basis quadrays, and developing the others using negation and vector addition -- we can simply "look them up by name" in the native class dictionary, which is named __dict__. We get this ability "for free", without needing to define any additional dictionaries and/or hashtables.
The interactive dialog below shows the user instantiating a new rhombic dodecahedron and querying the object's built-in dictionary:
Python 1.5.2 (#0, Apr 13 1999, 10:51:12) [MSC 32 bit (Intel)] on win32 Copyright 1991-1995 Stichting Mathematisch Centrum, Amsterdam >>> import polys >>> oRhdodeca = polys.Rhdodeca() >>> oRhdodeca.__dict__['F'] Vector(1, 0, 1, 1) >>> oRhdodeca.__dict__['G'] Vector(1, 1, 0, 1) >>>
As in earlier chapters, I'm using "quadray format" integrally within my class methods. In fact, this application uses quadray 4-tuples as the native format for the Vector object, by which I mean the data variable unique to each vector is a quadray 4-tuple. Tuples are "immutable" in Python, meaning you can't do in-place changes to their members (unlike lists, which are mutable). Using tuples for vector data helps ensure that my vector operations return new vectors, but without affecting the ones operated upon.