|
With the exception of a few corrected typos, the text which follows (including Notes)
is unchanged from its originally published form in the Buckminster Fuller Institute's
Synergetica Journal (ISSN: 1059-1486) Volume 1, Number 1 in late 1991 (there
were no subsequent issues). Some of the original artwork has been retained. The
wealth of new artwork and hyperlinks is a result of many talented individuals working
together on Computerizing Synergetics, an ongoing process.
| |
Synergetics in the 1990s | |
IntroductionR. Buckminster Fuller was best known for his geodesic domes. This fact has both helped and hampered our efforts to draw attention to his synergetic geometry, the "invention behind the inventions." Scientists will typically make the link between the shape of a virus or carbon molecule, and the dome's distinctive architecture, but then stop short of exploring the underlying tetrahedral geometry, because "architecture" is not virology or chemistry, and because "synergetics" is not in their vocabulary.
This paper is about some of the points of contact
between Fuller's explorations in what he termed "the geometry
of thinking" and contemporary developments in science and
mathematics. The recent isolation of a previously unsuspected
form of carbon, now popularly known as buckminsterfullerene |

|
|
Buckminsterfullerene combines with other elements
to form superconducting materials. The fullerene molecules may
be packed together like soccer balls in a face-centered cubic
lattice (fcp) while smaller non-carbon atoms, of potassium for
example, are interspersed in the octahedral voids.[1] Squeezing larger grades of atoms into the concavities pushes the fullerenes
slightly further apart, causing the material to superconduct at
higher temperatures, a property with potential commercial applications.
Sphere packing is at the heart of synergetics. What
chemists call the "face centered cubic lattice" Fuller
called the "isotropic vector matrix" - "isomatrix"
for short. The isomatrix may be modeled starting with a nuclear
sphere and packing successive layers of 12, 42, 92... |

|
|
When rods connecting the centers of adjacent closest
packed spheres are introduced, the skeletal lattice of the isomatrix
comes into view. The rods delineate tetrahedral and octahedral
cells. Twelve rods converge at each hub. Fuller saw the isomatrix
occurring everywhere in Nature and felt that humans needed to
wean themselves from an awkwardly cubic coordinate system if they
were to make a lasting success of themselves. Thanks in large
part to Fuller's pioneering efforts, the isomatrix is now at least
as prevalent as the geodesic dome in architecture and is known
to civil engineers as the "octet truss." The octet truss
was used to construct Biosphere 2 for example. Biosphere 2 is
a sealed structure permeable only to electromagnetic waves which
will be used to study the regenerative properties of an ecosystem
over a two year period. The experiment will include a cast of
human volunteers among its many animal subjects, making it an
obvious metaphor for the planet itself.
The octet truss is also very evident in the pavilion architecture at Epcot's Tommorowland where corporate purveyors of a high tech image are probably unaware to what extent Fuller's vision of the future has permeated their own. The centerpiece at Epcot is Spaceship Earth, a full geodesic sphere. Fuller's studies of geodesic structures began with axially spinning polyhedra and their characteristic great circle networks. Domes were derived as fractions of these spheres. All geodesic spheres based on the spherical icosahedron, Epcot's included, are characterized by their 12 pentagons and a variable number of hexagons. When the nodes at the centers of these hexagons and pentagons are dropped out, we the get the hexapents. Fullerenes, fly's eyes and turtle shells are among the hexapents found in Nature. A central dichotomy implied by these two architectural structures, the octet truss and the geodesic sphere (or buckyball), has to do with the symmetry groups to which each belongs. The isomatrix is home for structures sharing its 60 and 90 degree angles such as three of the Platonic polyhedra, the tetrahedron, octahedron and cube. Atomic lattices based on these angles appear unchanged when rotated by a half, a third, a quarter or a sixth of a 360 degree turn. The other two Platonic polyhedra, the icosahedron and pentagonal dodecahedron, contain the pentagon's 72 degree angles, and are therefore rotationally symmetric through a fifth of a turn.
|
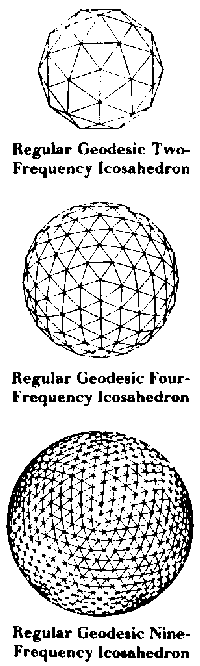
|
|
Mathematicians have proved that no structure with
five-fold or icosahedral symmetry will self-align when shifted
horizontally through space. No five-fold symmetric structures
are periodic. Since all crystalline structures were presumed to
be lattices, none with icosahedral symmetry were supposed to exist.
Landau and Lifshitz, an authoritative series of physics texts,
stated that icosahedral symmetry was "of no physical interest"
since it was thought never to be exhibited by inorganic matter.
This assumption later proved false when
quasicrystals
were discovered in 1982. (See: Incommensurable Icosahedra).
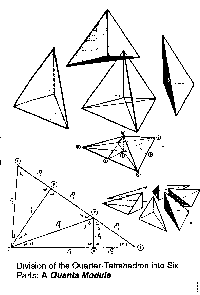
Analyzing the space of five-fold symmetric structures is the focus of many contemporary mathematical studies. Yasushi Kajikawa of the Synergetics Institute in Hiroshima has developed a non-periodic analog of the isomatrix called the "icomatrix," named for the icosahedron, which has been featured in the Japanese edition of Scientific American. Whereas the isomatrix consists of regular tetrahedral and octahedral cells, the icomatrix is comprised of five irregular cells of both varieties. Three lengths are sufficient to construct all ten cells: a unit edge, the radius of a unit-edged icosahedron, and phi. David Koski is another synergeticist whose as yet unpublished explorations center around phi-scalable tetrahedral modules developed by permuting seven edge lengths. One of these modules is the T-module, first introduced by Fuller in Synergetics 2. (See: Playing With Blocks). |
|
| Much of the background context for appreciating the general themes of synergetics is provided by the newly emergent field of design science. For example, in Connections: The Geometric Bridge Between Art and Science (McGraw-Hill, 1991), an early textbook on the subject, mathematician Jay Kappraff revisits an earlier time, when geometry, philosophy and art were more interpenetrating, and traces the intertwining historical trajectories of root2 (the diagonal of a unit square) and phi (the diagonal of a unit-edged pentagon). These numbers are the hallmarks of the crystalline and the quasicrystalline, the iso- and the icomatrix respectively. |

|
| Synergetics itself, as presented in the volumes Synergetics and Synergetics 2, is a deliberately metaphorical language, as much literary as mathematical, which strives to be both incisive and inclusive. At its focus are the exceptionless "generalized principles," akin to "natural laws," which Fuller tended to conceptualize as networks of great circles, their intersections comprising the universe of possible events. Stylistically, Fuller's writings and lectures tended to model his "spherical" approach to information retrieval by tending towards highly nonlinear formats that were nevertheless coherently systematic. Facilitating the formation of such "pattern integrities" within our exponentially expanding information base is what the so-called "hypermedia" are all about. Future presentations of synergetics will no doubt take advantage of this new technology to better convey a sense of nature's omniconsiderate "operational mathematics." (See: Computerizing Synergetics). |

|
|
| |