Exploring Groups and Codes
with Python

Part 1: Clubhouse Codes

Introduction

Cryptography provides a usefully practical application to go along with the more abstract concerns of a branch of mathematics known as group theory. Each topic casts light on the other which explains why they're frequently introduced in tandem -- just as I'm doing here. Additionally, with a very high level language in the picture, namely Python, we gain access to an interactive environment within which to investigate both the theory and the application.

I've become quite the evangelist for this "math through programming" approach to curriculum writing, having discovered that developing the material within the context of a command line interface (CLI) may provide that key "missing ingredient" which both catalyzes student understanding and motivates explorations of the concepts beyond what's presented in the text.

I provide more background regarding my evolving approach to curriculum writing in the For Further Reading section at the bottom of this page.

A Simple Cipher

A "clubhouse code" consists of simple letter substitutions. The shuffle method in random.py (part of the standard library) makes it easy and straightforward to generate a substitution dictionary:

"""
Set domain = string.digits if you want to work with
integers instead of printable letters -- or experiment
with other domains
"""
_domain = string.printable

def mkcode():
    """
    Return a string containing the elements in _domain
    randomly permuted
    """
    targ = list(_domain)
    shuffle(targ)
    return string.join(targ,"")

def mkdict(secretkey):
    """
    Turns _domain + secretkey into a dictionary of
    substitution pairs
    """
    keydict = {}
    j = 0
    for i in _domain:
       keydict[i]=secretkey[j]
       j += 1
    return keydict

The above utility, mkcode( ), returns a shuffled _domain suitable for use the string.mktrans( ) to generate a translation table. Python translation tables are strings of 256 bytes in some new order.

mkdict(key) pairs the _domain with the shuffled version to return a substitution dictionary. Were I dealing with playing cards, the resulting dictionary would randomly pair each card in Deck A with another in Deck B. Because both decks have an equal number of cards, no card is without its paired target -- which just might be the same card.

Usage:

>>> _domain = string.printable
>>> mycode = mkcode()
>>> mycode
'vOKiAYHXkDQmZfWwlGxIsduNJTrzPVocUbEjSgChnLqyFMaRpBte'
>>> mkdict(mycode)
{'z': 'T', 'x': 'N', 'y': 'J', 'v': 'd', 'w': 'u', 't': 'I', 
'u': 's', 'r': 'G', 's': 'x', 'p': 'w', 'q': 'l', 'n': 'f', 
'o': 'W', 'l': 'm', 'm': 'Z', 'j': 'D', 'k': 'Q', 'h': 'X', 
'i': 'k', 'f': 'Y', 'g': 'H', 'd': 'i', 'e': 'A', 'b': 'O', 
'c': 'K', 'a': 'v', 'Z': 'e', 'X': 'B', 'Y': 't', 'V': 'R', 
'W': 'p', 'T': 'M', 'U': 'a', 'R': 'y', 'S': 'F', 'P': 'L', 
'Q': 'q', 'N': 'h', 'O': 'n', 'L': 'g', 'M': 'C', 'J': 'j', 
'K': 'S', 'H': 'b', 'I': 'E', 'F': 'c', 'G': 'U', 'D': 'V', 
'E': 'o', 'B': 'z', 'C': 'P', 'A': 'r'}

So what's with _domain? It's a module-level variable intially defined as all printable charaters (= string.printable). But I might want to use integers or just uppercase letters as my domain. Integers are what the group theory people tend use when discussing permutations (i.e. substitution dictionaries). You can always have numbers serve as stand-ins for letters, or for any other kind of object, so moving to integers doesn't really change the basic mechanics of the situation.

Alternative usage:

>>> ciphers._domain = string.digits
>>> mycode = mkcode()
>>> mycode
'1639048572'
>>> mkdict(mycode)
{'8': '7', '9': '2', '6': '8', '7': '5', '4': '0', '5': '4', 
'2': '3', '3': '9', '0': '1', '1': '6'}

Permutation Notation

Mathematicians have come up with an alternative notation for representing the same information as in mycode.

Pick a number, any number to start, then worm your way through the dictionary, training each item to the one it maps to, e.g. using the above example, 8 maps to 7 which maps to 5 and so on through 4, 0, 1, 7 and finally back to 8. Now organize this loop into a tuple: ('8', '7', '5', '4', '0', '1', '6'), with the understanding that each member is followed by its pair, with the last member wrapping around to the first member, i.e. 6 maps to 8.

We aren't finished yet though, as we didn't get to all members with this single loop. 9 maps to 2 maps to 3 maps to 9 -- another cycle (loop), with no members in common with the first (speaking more technically, we can say the cycles are 'disjoint' meaning their intersection is the empty set).

Perhaps you will want to try writing a short Python routine that takes such a dictionary of unshuffled,shuffled pairs, as up top, and converts same to a list of cyclic tuples, as per the above example. The cycles2dict method included in the source module (ciphers.py) shows one possible solution.

Usage:

>>> p = cycles2dict(mkdict(mycode))
>>> p 
[('8', '7', '5', '4', '0', '1', '6'), ('9', '2', '3')]

And you'd want to make it bidirectional:

>>> dict2cycles(p)
{'8': '7', '9': '2', '6': '8', '7': '5', '4': '0', 
'5': '4', '2': '3', '3': '9', '0': '1', '1': '6'}

The thing to realize is that when a code pairs a letter with itself (or number with itself), you simply don't mention it in the cycles notation. Like, if it's the 'identity dictionary' (every letter is paired with itself), then the list of corresponding cyclic tuples is empty, and vice versa:

>>> dict2cycles({1:1,2:2,3:3,4:4})  # identity dictionary returns [ ]
[ ]
>>> ciphers._domain = string.uppercase
>>> cycles2dict([])
{'Z': 'Z', 'X': 'X', 'Y': 'Y', 'V': 'V', 'W': 'W', 'T': 'T' ... etc.}

Symmetry Groups

Group theory meets geometry when we consider symmetry groups. What rotations may we apply to a geometric shape such that it superimposes on itself? In other words, what rotations around what axes will permit you overlay the "before" and "after" pictures of a shape, and have them align perfectly?

When you rotate a square flat on the table by 90 degrees, it looks just the way it did before. You might also flip it over, like a pancake, and yet still have it look the same (except maybe the two sides have different colors). The same ideas apply not just to polygons (flat shapes) but to polyhedra (spatial shapes).

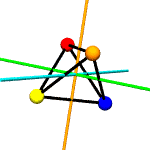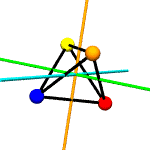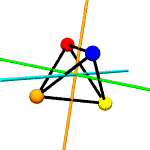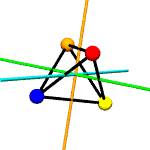
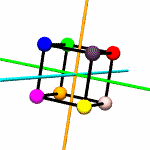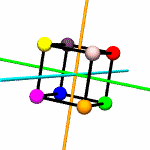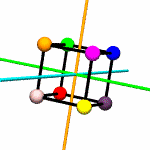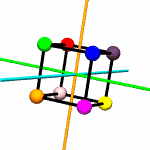
Think of colored spheres stuck on the four corners of a tetrahedron. We can use permutations to describe the ways these spheres might swap around with one another in ways consistent with rotation around various axes. The permutations act on the set of vertices.

For example, suppose you put a tetrahedron on a table and hold the apex fixed with your thumb, while rotating the base triangle 120 degrees. Three base spheres move to adjacent positions, with the 3rd coming round to occupy the position formerly held by the first. If these spheres were labeled A,B and C, the permutation might be expressed as [('A','B','C')]. The apex sphere, D, does not move, and so does not get mentioned in the permutation.

rotations.py contains a Tetrahedron class which does little more than write itself out to a file intelligible to POV-Ray, a free ray tracing program. Accompanying this class are the 12 possible permutations, including the identity permutation (every sphere stays as it is), which describe the tetrahedron's symmetry group.

>>> otet = rotations.Tetrahedron() # tet object
>>> otet.listp()  # tet: 12 permutations
Permutation: [('B', 'C', 'A')]
Permutation: [('D', 'A', 'B')]
Permutation: [('B', 'A', 'C')]
Permutation: [('D', 'B', 'A')]
Permutation: [('D', 'A', 'C')]
Permutation: [('D', 'C', 'A')]
Permutation: [('D', 'B', 'C')]
Permutation: [('D', 'C', 'B')]
Permutation: [('D', 'C'), ('B', 'A')]
Permutation: [('D', 'B'), ('C', 'A')]
Permutation: [('D', 'A'), ('B', 'C')]
Permutation: []
>>> rotations.genpix(5,otet) # take random snap shots

By applying these 12 permutations, or products of these permutations (multiplication is defined below), to our tetrahedron, we move its vertices around among fixed positions. Any product of these 12 permutations will likewise be one of the 12. This closure property, where the product of any two elements in a set gets another element in the set, is essential to any group, as are some other properties discussed in the next section.

Notice that not all conceivable permutations are included among the 12. A pair of spheres with a shared edge between them might swap, leaving the other spheres where they are. But there is no conceivable rotation of the tetrahedron that would accomplish this. Such a permutation changes the "handedness" of the tetrahedron, as when a left handed glove is turned inside out to make a right handed glove. This is more than simple rotation can accomplish, and so such permutations are excluded from this particular list, which is meant to describe rotations.

>>> oc = rotations.Cube()
>>> rotations.genpix(10,oc) # cube: 24 permutations

Encrypting a Message

Back to cryptology: if we use simple letter substitution, with the same new letter always taking the place of the same old letter, then certain patterns will clue the would-be code cracker. Palindromes, which spell out the same sentence forward and backward, will still be palindromes, even if nonsensical.

Consider the encrypt method: it simply takes one of these substition dictionaries (a.k.a. permutations) and does the swap, ignoring any characters/punctuation/other symbols that aren't being converted. The decrypt method simply reverses this process.

def encrypt(plaintext,secretkey):
    """
    return ciphertext using the substitutions in _domain
    returned by mkcode()
    """
    table = string.maketrans(_domain,secretkey)
    return plaintext.translate(table)

def decrypt(ciphertext,secretkey):
    """
    decryption = encryption with reversed substitution
    """
    table = string.maketrans(secretkey,_domain)
    return ciphertext.translate(table)

So you can go:

>>> import ciphers
>>> from ciphers import *
>>> import string
>>> ciphers._domain = string.letters
>>> mycode = mkcode()
>>> mycode
'qhKnxipdwTcmbDUfrVCEvBWlHGFtPOYaRsQZeNzJjkXISyLMugoA'
>>> dict2cycles(mkdict(mycode))
[('z', 'G', 'R', 'I', 'Q', 'X', 'g', 'p', 'f', 'i', 'w', 'W', 'u', 'v', 
'B', 't', 'E', 'Y', 'o', 'U', 'L', 'N', 'J', 'Z', 'A', 'F', 'a', 'q', 
'r', 'V', 'M'), ('x', 'l', 'm', 'b', 'h', 'd', 'n', 'D', 'O', 'j', 'T', 
'y', 'H', 's', 'C', 'P', 'k', 'c', 'K', 'e')]
>>> e = encrypt("Able was I ere I saw Elba", mycode)
>>> e
'Fhmx WqC Q xVx Q CqW Ymhq'
>>> decrypt(e, mycode)
'Able was I ere I saw Elba'

Notice that the encrypted palindrome is still a palindrome. That makes is a lot easier to crack. A more sophisticated enciphering system would find a way to eliminate such clues to the would-be code breaker.

Multiplying Permutations in a Group

Back to group theory: we can multiply permutations together, meaning if you scramble a scramble, you get another scramble. For example if p1 is [('A','C','D')] and p2 is [('A','D','C')] then p1 * p2 means we apply p1 and then p2 to the result i.e. in p1, A maps to C which, in p2, maps back to A, so, in the end, p1 * p2 maps A to itself.

Likewise, D goes to A which maps back to D, so D maps to D, and yes, C maps to C. So p1 and p2 are really multiplicative inverses of one another, since their product is the identity permutation (that's the definition of inverse pairs -- their product is the identity e, where p1 * e = e * p1 = p1).

So it makes sense to design a Python class that makes these permutations into objects, which we can then multiply together using an overridden * symbol. We'll define __mul__ and __pow__ -- the latter because a permutation can also permute itself, as many times as we like. We'll also define __div__, since division by p1 may be viewed as multiplication by the inverse of p1, i.e. p1.inv( ).

Here's what this looks like:

>>> dict1 = cycles2dict([('A','C','D')])
>>> dict1
{'C': 'D', 'D': 'A', 'A': 'C'}
>>> cycles2 = [('A','D','C')]
>>> cycles2dict(cycles2)
{'C': 'A', 'D': 'C', 'A': 'D'}
>>> p1 = P(dict=dict1)     # create permutation objects...
>>> p2 = P(cycles=cycles2) # using code dictionaries or lists of cycles
>>> p1*p2       
Permutation: []

Note: Permutation: [ ] is the empty list, i.e. the identity permutation -- the expected result.

Multiplication goes left to right i.e. one applies the permutations in the order one would read them (assuming one's writing system is likewise left to right). On the other hand, a composition of functions syntax would work from the innermost function outward, which is effectively right to left. Python affords us the option of using such notation by allowing the __call__ method to define how objects should behave when followed by parentheses. Instead of writing p1 * p2 * p3, we might write p3(p2(p1)).

>>> e,p1,p2,p3 = P([]),P(),P(),P() # P([]) returns the identity element
>>> p1*p2*p3 == p3(p2(p1(e)))      # these two expressions equal
1

This idea of multiplying permutations, raising them to powers and taking their inverses suggests we might create a more elaborate enciphering strategy wherein multiple permutations get raised to higher and higher powers, plus form a product, to give a new substitution dictionary with each letter to be enciphered -- a reversible process (or one would hope).

We will return to this idea at the end of Part 2.

For further reading:

• Parts 2, 3 and 4 of Exploring Codes and Groups with Python
• Source code for ciphers (py and html versions)
• Source code for rotations (py and html versions)
• Background thinking re this essay
• Trends in Early Math Learning
• Clubhouse Crypto

Return to CP4E

Oregon Curriculum Network