Trends in Early
Mathematics Learning:
Looking Beyond Y2K
by Kirby Urner
First posted: Sept 13, 1999
Last modified: Aug 30, 2000
Version 2.2
Data Structures and Methods
Mathematics notations through the ages have served the dual purpose of representing stored values on the one hand, while signifying operations with those values on the other. At the most general level, we've always needed to communicate both static and dynamic aspects of systems. Data structures provide a snapshot of a particular state, while operations correspond to rule-based changes which move us from one state to the next.
Variables, matricies, lists, tuples, queues, stacks, trees and simple numerals are data structures. A matrix, for example, is an indexed array with rows and columns, just as a vector is a single row or column, or tuple. Numerals use place value with respect to some base for structure, and perhaps a sign (positive or negative). Historically speaking, this way of representing numbers developed in close association with the abacus, a state machine for storing numbers and facilitating arithmetical operations on them.
Data structures (a kind of artifact) may be defined around geometric or topological attributes. The unit circle and XYZ apparatus are examples of such structures, against the backdrop of which the operations of sin and cos or * -- as in 4 * (1,0,0) -- take on their well-defined meanings. Directed graphs and binary trees likewise have their visual or diagrammatic representations.
Operations include the familiar unary and binary functions, such as we find on scientific or financial calculators, plus any number of user-defined functions (or relations) accepting a wide assortment of inputs, including switches or options (what we encounter in a command line environment as arguments, typically stored to variables as a first action of any program).
As students increasingly gain access to a command line environment, I anticipate early mathematics will evolve its already well-entrenched concept of set (e.g. a set of tuples pairing a function's inputs and outputs) into a more nuanced investigation of this wider range of collections and data structures.
Students will explore these structures in complement with the characteristic operations associated with each. For example, the matrix structure comes bundled with methods for extracting a single row or column, for swapping rows, for transposing around the diagonal and so on.
The Impact of Object Oriented Modeling in Early Math Learning
These packages of data + methods are what software engineers now call objects. Objects instantiate classes in a class hierarchy defining lines of inheritance. I consider it somewhat inevitable that the early mathematics curriculum will be significantly impacted by this objects concept, which by this time completely permeates commerce and industry, thanks in large degree to the global internet.
The impact of object-oriented modeling on early mathematics teaching may be associated with some important secondary trends, which likewise have to do with the interface between mathematics and computer technology:
-
algorithms (methods) associated the various data structures need not be about numeric values exclusively i.e. the data may well be non-numeric in character, yet nonetheless amenable to rigorous symbolic processing (e.g. sorting)
- the necessity for training with these concepts, including in the early grades, is combining with the computer's lowered cost to make access to the command line an infrastructural requirement of math classes at all levels (which command line is usable for non-numeric as well as numeric symbolic processes).
In sum, the focus on objects as entities which encapsulate both data and methods, is changing the mix of concepts deemed most relevant even in the early grades, but in such a way as to permit a smooth transition from older, time-tested approaches to the material -- provided curriculum writers do their homework.
As I indicated above, set theory and the theory of data structures easily blend together, with filtered retrieval using boolean expressions, concepts of union and intersection having as much application to lists and tables as to sets. With tables, we get the concept of primary keys and a relational database model (rules of normalization) -- structures with more properties and operations than "pure" sets necessarily define, and therefore presentable as subclasses of this more generic superclass concept.
From this curriculum node (evolved from the pre-existing set theory node), we will naturally branch into SQL (standard query language) and give students some valuable insights into what a database engine is all about, and how these interface with users (via the web, via ATMs) in the real world.
The move to command line access at every desk is a natural step to make post the introduction of calculators at all levels (a step already taken), which calculators will need to be displaced and/or supplemented because of their inferior capabilities with respect to non-numeric data in the context of an object oriented approach.
None of the above is especially controversial I don't think -- I am mostly extrapolating from existing trends, already well-evident in many teaching environments, especially at the college level. However, one might further speculate as to how the object oriented model is going to feed back to impact mathematics more generally at the higher levels, especially once we have new generations of professionals schooled to think along these lines since first or second grade.
The Effects of Object Modeling in Higher Math
For example, I think most mathematicians today are content to think of a quaternion as simply the data structure, a 4-tuple with real and complex members, with a vector part and a scalar part. This is to reserve the name quaternion for the data structure alone, while externalizing the methods as somewhat freely floating functions inherited from a superclass of more generic operations, which would include addition and vector multiplication, customized to work with these particular data.
Although this view is in no way "incorrect", I think we might be developing a new bias in our mathematicians, thanks to object orientation, whereby the quaternion label grows to encompass the operations, just as vector will grow to include vector operations. The methods of inner and outer product will therefore "belong" to the same object as the data itself i.e. operations and data will become part of a single parcel or object -- the vector object. Quaternions then might be presented as a subclass of multivector, if thinking in terms of a Clifford Algebra, with methods for inner and outer product overridden to implement Hamilton's way of dealing with these things.
Fig 1: Quarternion-Driven Cube by K. Urner
At the notational level, what this looks like is making methods
attributes of objects. So whereas in the past we would have
written:
q3 = q1 * q2 (product of two quaternions)in future text books, we're maybe as likely to see:
q3 = q1.mult(q2)where the mult method is an attribute of any quaternion, is contained within the quaternion object (which consists of methods, not just data).[1] More subtly, we could even use the first kind of notation but see the * (multiplication operator) invoking a method internal to q1 or q2 -- because in some languages (e.g. Python and C) we have the ability to "override" the primitive symbols and supply our own implementations, internally to a class. This permits continuing use of the classical notations in the context of an OOP model.[2]
Even if students don't yet know what quaternions are, or how to operate with them, having diagrams which describe entities as subclasses of one another will likely prove illuminating.
The Importance of Non-Numeric Methods
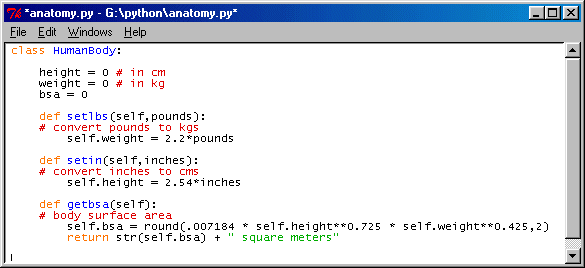
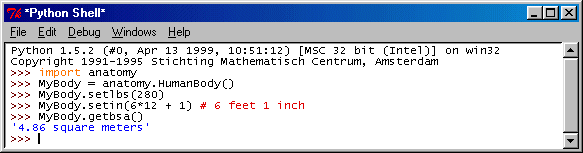
Returning to my original points, we need to start early with concepts involving indexed data structures especially. A level one text would include such obvious syntax as:
>>> AlphaList = ['C','A','T'] >>> AlphaList[0] 'C' >>> AlphaList[2] 'T'I leave it to others to argue whether indexing from an origin of zero or one is "best" -- probably students should be advised early on that both methods are common conventions and should get plenty of practice in using both.
I've used a command line format above, which is inherently a dialog between user and computer. User commands are requests for action, tell the circuits to execute various instructions. Results are expected -- or an error message, if the syntax is incorrect and the computer is unable to parse the request into a sensible executable.
Note that I'm deliberately using non-numeric data in the above example. This is important. A matrix or 2-dimensional array might just as well contain names of fruits or vegetables. From a pictorial standpoint, this is appealing. We could display a 3x3 matrix with a vegetable depicted at each (row,column) location. A simple command line system might come back with the picture itself, captioned with the name of the vegetable at MyVeggies[2,1].
Polyhedra as Paradigm Objects
Polyhedra are objects in the traditional sense, but also in the object oriented sense: they consist of data and methods. Polyhedra have vertices scattered in space. This gives you (x,y,z)-formatted or other tuples, perhaps organized in a list. Plus polyhedra grow or shrink (are scalable), rotate (around an axis -- defines a corresponding equator), and translate (shift laterally without any other change in size and/or orientation).
Polyhedra should also have methods for keeping track of their own volumes and surface area, as well as their current "center of gravity" and orientation relative to a "world" system of coordinates. Features such as "color" may also be specified, though traditionally considered "secondary attributes" in philosophical jargon. Computer languages encourage us to pay attention to secondary, as well as primary attributes.
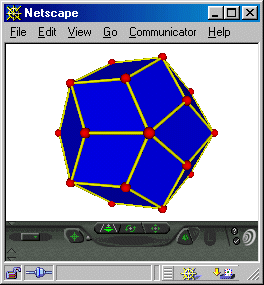
Fig 2: VRML view: Rhombic Triacontahedron
Giving students a complete grasp of these methods, at the programming level, is a worthy goal to aim for, as it will end up requiring forays into trigonometry, analytic geometry, and vector and matrix algebra. Given this will be undertaken in a real computing environment, students will have access to colorful ray traced results of their scripts or programs, plus the ability to inspect their geometries using a VRML plug-in in their web browser.[3]
Learning to represent polyhedra in VRML notation would be another curriculum goal, according to this model -- perhaps not in any excrutiating detail (some students will become very interested in this content, others not at all -- a spectrum), but in such a way as to impart appreciation for how data is translatable into a variety of formats, depending on who or what the target "reader" might be. Conventional text book math notations are "just one more format" targetted at those trained to read conventional math notations.
I'm not suggesting that polyhedral geometry be the one and only "be all and end all" for a K-12 mathematics curriculum, merely that this could and should be a strong thread, a kind of "backbone" of interlinked concepts, naturally organized around a visual/tactile and ancient tradition where much is already known and well communicated.
Moving Beyond Flatland
Opening the world of spatial geometry to students is what I call the beyond flatland approach, which is not to eschew some use of Euclidean style proofs ala the more typical plane geometry approach -- but as a means to an end.[4]
Too often we leave the polyhedral stuff for the end of the year, and never get to it. Then geometry disappears from the scene, only to resurface implicitly when we start using the calculus to solve a few volume problems, or maybe do a section on vectors, usually only in the form of "force diagrams", which, again, are usually done in a plane at the high school level.
To avoid spatial geometry so completely bespeaks of a glaring weakness in K-12 in my estimation. The real world is spatial, with both natural and architectural forms being volumetric, not flat. Geometry textbooks often tantalize students with pictures of the spatial geometries relevant to so many disciplines, but rarely go there in practice, except maybe in the side bars or in chapters the teacher doesn't get around to, or in the optional reading sections (students never have time to follow up, although if the reading were a clickable URL in some hypertext article, they just might).
In addition to whatever screen renderings or "VRMLizings" of polyhedra we might generate from the command line environment, the groundwork for these experiences needs to be laid in the more tactile medium of hands-on model making. This is where we develop motor skills, being able to cut straight with scissors, to use glue in moderation. We also learn to appreciate strategies for structuring, using our own imaginations, and by working with the various kits or toys supplied to us -- even if our "kit" is simply dried peas and toothpicks, or gum drops and wooden dowels.
It's in the realm of working with physical models that students develop some confidence in their ability to manipulate real objects, not just screen based or computerized ones. Plus these operations of rotation and translation are completely accessible to even the very young, once any real world object is brought into play -- but preferably one constructed by the student. Then comes the concept of rotational symmetry: how rotating a shape by a certain increment allows it to seamlessly juxtapose with its unrotated self. Or in the case of a lattice: how a shape may be translated (without rotation) by some increment, and found periodically throughout space (again, juxtaposition or congruence is a way to show identity in shape).
My testing of hands-on activities using various supplies, including clay, wooden dowels with rubber joins, and paper, proves the cross-cultural appeal of making polyhedra. I've done it with 3rd-4th graders in Bhutan, 4th-6th graders in Lesotho, and with comparably aged children in Portland, Oregon. This last group was especially unpracticed in the use of scissors however, leading me to wonder if these kinds of hands on activities had fallen out of favor in the lower grades.[5]
Speaking of lattices, here is where my school of thought in
particular has chosen to innovate away from the curriculum norm.
Given familiarity with polyhedra (their hands-on construction and
programming as objects) as a central curriculum goal, we find it
advisable to get into sphere packing early in a student's
training.
The lattice formed by closest-packed spheres provides a somewhat more natural context in which to embed common polyhedra than does the more rectilinear XYZ lattice. This sphere packing lattice is more "with the grain" of more polyhedra and modeling kits with the requisite 12-valency hubs make a lot more shapes.[6]

Fig 3: Closest packed spheres
Given three spheres packed intertangently, a fourth most naturally
nests in the "valley" formed by these three, providing the fourth
vertex of a regular tetrahedron. This tetrahedron is structurally
stable and is the most primitive sharply featured volume (vs. some
blob, like a sphere), i.e. has the fewest edges, vertices and faces
of any container, the cube having 12 edges, 8 vertices and 6 faces,
as compared with the tetrahedron's 6, 4 and 4 (Euler: E-V=F-2).
So the inherently 60 degree coordination associated with sphere packing begets a tetrahedron right off the bat. We have the option to use this tetrahedron as our unit of volume, to stream-lining effect, when developing our concept of a concentric hiearchy of lattice-embedded polyhedra.[7]
Although it's true that cubes space-fill and thereby provide a very simple lattice, over-emphasis on XYZ to the exclusion of the fcc lattice (a.k.a. the isomatrix in our curriculum) is a barrier to appreciating non-90-degree based spatial relationships. The regular tetrahedron deserves equal time, and of course diagonalizes the cube, meaning it's not really a problem to bridge the two lattices and regenerate them as both aspects of the same uniform distribution of reference points, or volumetric pegboard, into which our other polyhedra may be inserted (including programmatically, using any of several data formats to store the vertices relative to some origin on computer).[8]
A Backbone of Integrated Concepts
To summarize: our 21st century K-12 math curriculum:
-
features command line access for all students (with specialized enchancements for those with disabilities of various kinds)
-
promotes thinking in terms of objects as data structures plus methods for performing operations on that data
-
uses polyhedra as paradigm objects, and
- encourages hands-on modeling in various materials as a way to bridge the gap between the ephemeral screen-based world of the computer and the everyday world of physical objects.
I have given definition to this central "backbone" of integrated concepts not because I want to exclude important math topics not explicitly touched on above, but because I see this as a way of creating a framework or superstructure to which other topics traditionally covered may be constructively attached.
For example, we typically would get to polynomials, the quadratic equation, binomial theorem, sigma notation, probability and statistics before the end of a standard high school curriculum. How would these fit? And what about the calculus?
My own approach, to take one example of a solution, has been to take simple sphere packing, already introduced with an eye towards defining the isomatrix, as a basis for introducing square and triangular numbers. These come in sequences i.e. (1,4,9,25...) and (1,3,6,10,15...) respectively, and to these sequences there correspond their cumulative (i.e. running total) sums through N terms.