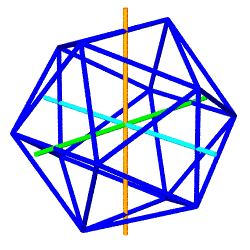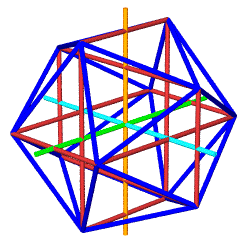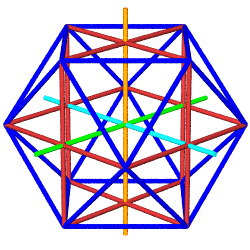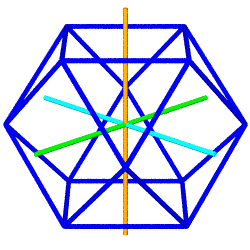
The Python module used to
generate these animated GIFs (above right) takes object-oriented
programming one step further, by having the Icosa and Cubocta subclasses
inherit data and methods from parent classes Shape and Jitterbug. Here we
have an example of "multiple inheritance", with some shapes getting
the Jitterbug methods, others (such as Tetra and Cube) just inheriting from
Shape.
As both of these subclasses inherit from Jitterbug, they
get a list of edgepairs, which organizes 24 edges into 8
triangles. Every edge pairs two of 12 vertices obtained from three
mutually perpendicular rectangles. These 12 vertices are stored in
vertdict.
class Jitterbug:
# Edges of 8 triangles defined by the 12 vertices generated
# as the corners of (a) root2 x root2 squares (cuboctahedron)
# or (b) 1 x phi rectangles (icosahedron)
edgepairs = [['Axy','Axz'],['Axz','Ayz'],['Ayz','Axy'],
['Axy','Dxz'],['Dxz','Byz'],['Byz','Axy'],
['Bxy','Bxz'],['Bxz','Ayz'],['Ayz','Bxy'],
['Bxy','Byz'],['Byz','Cxz'],['Cxz','Bxy'],
['Dxy','Axz'],['Axz','Dyz'],['Dyz','Dxy'],
['Dxy','Dxz'],['Dxz','Cyz'],['Cyz','Dxy'],
['Cxy','Bxz'],['Bxz','Dyz'],['Dyz','Cxy'],
['Cxy','Cyz'],['Cyz','Cxz'],['Cxz','Cxy']]
def mkrect(self,v1,v2,tag):
# add four rectangle defined by vectors to vertdict with
# keys 'A','B','C','D' + passed tag identifying plane
# of the rectangle i.e. 'xy','xz' or 'yz'
# Rectangle is: square when v1,v2 come from cuboctahedron
# " ": golden (1xphi) when v1,v2 from icosa
self.vertdict['A'+tag] = v1 + v2
self.vertdict['B'+tag] = -v1 + v2
self.vertdict['C'+tag] = -v1 - v2
self.vertdict['D'+tag] = v1 - v2
Where the shapes differ is in the dimensions of these three
rectangles: 1 x phi (golden rectangles) in the case of
the icosahedron, Root(2) x Root(2) in the case of the
cuboctahedron. These differences show up in the subclass
definitions:
|
class Icosa(Jitterbug,Shape):
def __init__(self):
# make 3 golden rectangles
# of 1 x phi in the
# xy, xz and yz planes.
# The resulting vertices
# will be those of the
# icosahedron
# xy plane
tag = "xy"
v1 = Vector((0.5,0.0, 0.0))
v2 = Vector((0.0,phi/2.0,0.0))
self.mkrect(v1,v2,tag)
# xz plane
tag = "xz"
v1 = Vector((phi/2.0,0.0,0.0))
v2 = Vector((0.0, 0.0,0.5))
self.mkrect(v1,v2,tag)
# yz plane
tag = "yz"
v1 = Vector((0.0,0.0,phi/2.0))
v2 = Vector((0.0,0.5,0.0))
self.mkrect(v1,v2,tag)
|
class Cubocta(Jitterbug,Shape):
def __init__(self):
# make 3 squares
# of root2 x root2
# in the xy, xz and yz planes.
# The resulting vertices
# will be those of the
# cuboctahedron
# xy plane
tag = "xy"
v1 = Vector((root2/2.0,0.0,0.0))
v2 = Vector((0.0,root2/2.0,0.0))
self.mkrect(v1,v2,tag)
# xz plane
tag = "xz"
v1 = Vector((root2/2.0,0.0,0.0))
v2 = Vector((0.0,0.0,root2/2.0))
self.mkrect(v1,v2,tag)
# yz plane
tag = "yz"
v1 = Vector((0.0,0.0,root2/2.0))
v2 = Vector((0.0,root2/2.0,0.0))
self.mkrect(v1,v2,tag)
|
|
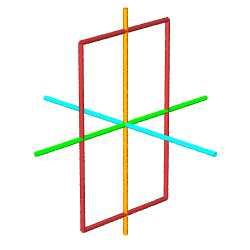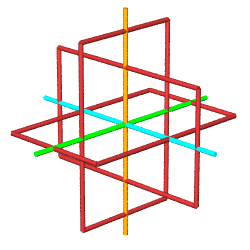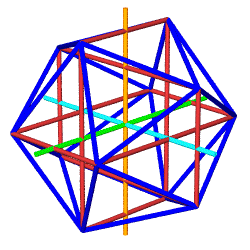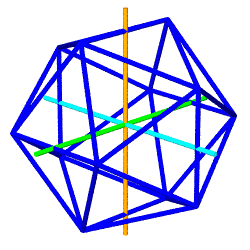
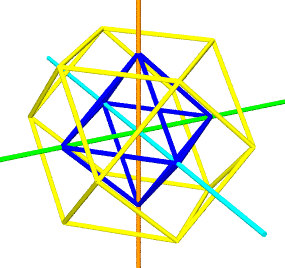
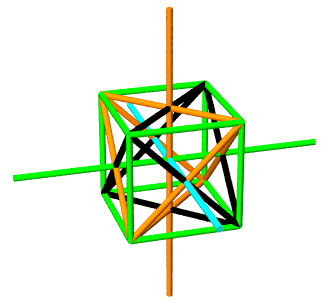
The yellow cuboctahedron shown above is defined by 12 vectors
from the origin, all of the same length. The same 12 vertices may
be obtained by tightly packing 12 spheres around a nuclear sphere.
Given we have set the distance from the origin to any of the
surrounding vertices at 1, it follows that the spheres have a
diameter of 1, a radius of 1/2.
>>> import shapes
>>> ocubocta = shapes.Cubocta() # define a cuboctahedron
>>> radii = [] # empty list
>>> for i in ocubocta.vertdict.values(): # step through vertices...
radii.append(i.length()) # ...adding lengths to list
>>> radii # show list
[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]
>>> oCubocta.volume()
20.0
In the last section of this essay, we briefly
introduce the
Qvector and
Svector subclasses of Vector, which are
initialized with quadray and spherical coordinates
respectively. Below is a table listing the quadray and spherical
coordinates of the yellow cuboctahedron shown above. A few similar
utilities for listing formatted data are appended to the end of shapes.py.
>>> def table():
print " quadray spherical " # header line
print "-------------------------------------" # header line
for i in ocubocta.vertdict.values():
print "%s %s" % ((i.quadray()),(i.spherical())) # data lines
>>> table()
quadray spherical
-------------------------------------
(2.0, 1.0, 1.0, 0.0) (1.0, 45.0, 90.0)
(0.0, 2.0, 1.0, 1.0) (1.0, 90.0, 135.0)
(2.0, 0.0, 1.0, 1.0) (1.0, 90.0, 45.0)
(0.0, 1.0, 2.0, 1.0) (1.0, 135.0, 180)
(0.0, 1.0, 1.0, 2.0) (1.0, 135.0, -90.0)
(2.0, 1.0, 0.0, 1.0) (1.0, 45.0, 0.0)
(1.0, 1.0, 0.0, 2.0) (1.0, 90.0, -45.0)
(1.0, 0.0, 1.0, 2.0) (1.0, 135.0, 0.0)
(1.0, 0.0, 2.0, 1.0) (1.0, 135.0, 90.0)
(1.0, 2.0, 1.0, 0.0) (1.0, 45.0, 180)
(1.0, 2.0, 0.0, 1.0) (1.0, 45.0, -90.0)
(1.0, 1.0, 2.0, 0.0) (1.0, 90.0, -135.0)
Looking in the spherical column, we find all vectors are of
length 1.0 (as expected), with three groups of four vectors each at
45, 90 and 135 degrees from the
Z-axis in the YZ plane. These correspond the the
four squares perpendicular to the orange Z-axis in the above rendering, with the
equatorial square consisting of root(2) face diagonals (not part of
the figure). Each group contains two pair of oppositely pointing
vectors in the XY plane,
e.g. 90 and -90.
Quadrays derive from four basis rays pointing from the origin to
the four corners of a regular tetrahedron, labeled
(1,0,0,0)(0,1,0,0)(0,0,1,0) and (0,0,0,1). This tetrahedron is
constructed from four closest-packed equiradius spheres. Given we
have assumed unity as the sphere diameter, these spheres have a
radius of 0.5, and the tetrahedron has edges of unit length. The
twelve cuboctahedral vectors, expressed in quadray format, consist
of all permutations of {2,1,1,0} -- note that we do not need
negative numbers, no matter which way a vector points from the
origin.
Some of the vector-based algorithms we will find especially
useful in the next section use the
Povray class methods to display a triangular sphere packing with a
user-specified number of rows. For example, tripack centers
the packing over the origin, and places the bottom row of spheres
along the x-axis. The code below shows a function making use of
tripack (see module).
|