WE SHALL OVERCOME

REGARDING THE USE OF A VERY HIGH LEVEL LANGUAGE
IN THE PRE-COLLEGE MATHEMATICS CLASSROOM

by Kirby Urner
Oregon Curriculum Network
First posted: January 13, 2001
Last updated:November 13, 2005

Table of Contents:

First posted to the Python edu-sig with a copy to math-teach

OVERCOMING A PREJUDICE

Yes, I think it’s mostly just a prejudice that math teachers have against mixing programming languages with their "pure" math language.

They’re still thinking back to the days of punch card FORTRAN (some of them), or basing their conclusions on trying to program a TI -- neither experience being that great a basis upon which to judge what it’d be like to use a VHLL (very high level language) like Python in the math classroom.

THE CASE OF APL

I don’t know how much exposure Guido had to APL (A Programming Language) before coming up with Python, but in my own case, APL was the first real computer language I ever learned (not counting programming my friend’s dad’s HP-65 calculator when in high school). In those days, most programming really was still with punch cards, and APL was one of the few languages offering an "environment" -- a place to interact with the language at a command line, in a "you type, computer responds" session. All around campus, including in my dorm, were these "APL terminals" connected directly to the IBM 370 at the computer center. Instead of normal keyboards, they had these weird greek-looking squiggles for upper case options. These were the APL symbols.

APL originally evolved as a chalkboard notation. It could easily "pass" for a math notation, because that’s exactly what it was, to start. Kenneth Iverson wanted a math notation that could be implemented directly in an interpreted environment. A single operator, like i (squiggly-looking i) would output a list of values, like i(6) meant (gave you) [0,1,2,3,4,5] -- or something like that (I forget if 6 was included, or if the values really had commas in between, or just spaces -- doesn’t matter right now).

Using APL notation, you could express rather involved mathematical operations in a single line, just as you can with regular "pure" math typography. APL, like text book math notation, is highly "crypto-compressed". Perhaps too crypto-compressed -- which is one reason why it failed to take the programming world by storm (I think Princeton had all those APL terminals around campus because some anticipated that it might -- this is 1976-77, and APL seemed like the wave of the future).

PYTHON AS "MATH LANGUAGE"

Python is, in a lot of ways, a lot like APL. Instead of i(6), you write range(6). The greek-looking symbols have been replaced with old fashioned English-type words. But you can still build with them, like Legos™, to make rather complex expressions. The basic built-in functions and operators fit together in all kinds of interesting ways; the language is highly "orthogonal" as computer scientists like to put it.

So what I think about Python is that it’s really another math language, like APL was/is -- not "just" a programming language. By this I mean, it’s human-readable, a way to capture math concepts and algorithms in a communicative format, just as math typography is. A VHLL like Python isn’t just about "talking to machines", it’s about "talking to other humans" (and it's machine-executable -- as are conventional math typographies these days, in packages such as MathCad).

And so if you’re having some trouble getting what’s going on using the conventional math typography, then here’s Python, executable, interactive, and likewise fairly concise, giving you a second chance, an alternative approach, a different way of saying the same thing. I think for a lot of students, it’s the introduction of an alternative entré that will make math come alive. It’s like being able to "see in stereo" all of a sudden, because now you have two images, each from a slightly different angle. This can make a world of difference.

CASE STUDY: SIGMA NOTATION

Consider sigma notation: a capital greek Sigma (somewhat alien-looking to students, as we don’t teach Greek anymore in most curricula, the "classical education" template having been long ago abandoned in large degree), followed by some expression with indexing in it -- some i, or j, to be successively replaced with successive integer values, starting and stopping according to what’s written at the bottom and top of the sigma sign (note: other variants of this notation just use the space at the bottom).

And so we write:

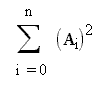
This is a specific Sigma expression, and involves raising successive terms to the 2^nd power, and summing them ("to sigma" is "to sum").

But the above expression is not something you can "do" yet.

We don’t know what n is, nor what the sequence A looks like. So to actually generate a value corresponding to the above expression, you have to define both n and A. These then become your "parameters", are the variables relative to which the above expression makes sense.

Now consider the same concept using Python:

         def Sigma(A,n):
              sum = 0
              for i in range(n+1):
                  sum = sum + A[i]**2
              return sum

So far, this is as general as the Sigma version, as we haven’t defined either A or n. Translation involves understanding the range() function -- outputs a list up to but not including the single argument (2 or 3 argument forms an option -- see below). So we say range(n+1), i.e range(3) -> [0, 1, 2].

So let’s consider A to be a sequence of numbers:

A[0] = 1, A[1] = 3 A[3] = 5 A[4] = 7...

Looks like the odd numbers. OK, A = odd numbers. Now we just have to decide how many of them we want. Let’s say n = 10.

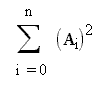where n=10, and A[0]=1, A[i] = 2i+1
Result: 1771

Now in Python (>>> is the prompt, where the user types, with blue lines flush to the left being what the computer answers):

>>> A = range(1,100,2)
 >>> A
 [1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 
 29, 31, 33, 35, 37, 39, 41, 43,  45, 47, 49, 51, 
 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 
 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99]

... another use of range(), from 1, to 100 -- (not including 100) , step by 2.

 >>> Sigma(A,10)
 1771

OPERATING ON OPERATORS

Notice that we expressed the set of odd numbers using a rule, in the Sigma example. A[i] = 2i - 1. That’s interesting, as it suggests turning A into a function of i.

 >>> def A(i): return 2*i - 1

 >>>  A(10)
 19

Let’s rewrite the sigma function to accept a function as a parameter. This is starting to get interesting, because any higher math teacher will tell you that students often have conceptual difficulty trying to look at functions as objects of other operators. Yet that’s what we’re going to do:

          def sigma(A,n,start=0):
                 sum = 0
                 for i in range(start,n+1):
                       sum = sum + A(i)**2
                return sum

Notice the subtle difference: ‘A’ is coming in as a function, and A(i) is derived by working the function using ‘i’ as input, where the initial value of i is set by the start variable (which here defaults to 1). Sigma also now allow us to pass the starting value for i as a parameter. Since A(i) returns -1 when i=0, we will pass a starting value of 1.

Interactively now:

 >>> Sigma(A,10,1)
 1330

Now write another function named B for the even numbers:

 >>> def B(i): return 2*i

 >>> Sigma(B,10,1)
 1540

Remember, our specific sigma expression (above) is summing the 2^nd powers of the terms generated by A(i) or B(i). Since this isn’t really what Sigma means by itself, generically, it makes more sense to define Sigma as simply the sum of whatever terms.

We can do this even more succinctly using orthongonal "Lego™ language" constructs:

 >>> from operator import add, mul  # mul used later in Pi
 >>> def Sigma(f,n,start=1):
         return reduce(add,[f(x) for x in range(start,n+1)])

The use of f is specifically designed to have us think ‘function’. To map a function is to apply it to the list that follows, i.e.

map(f,[1,2,3,4,5]) = [f(1),f(2),f(3),f(4),f(5)]

To reduce with an operator is to go ((((1 op 2) op 3) op 4) op 5) whatever op might be, in this case add (+).

So if we want to sum the squares of the first 10 odd numbers, the burden of generating these terms should be on f:

 >>> def f(x): return (2*x - 1)**2

Then pass this as a parameter to sigma:

 >>> Sigma(f,10,1)
 317338

Or change f to make it return the 2nd power of the ith even number:

 >>> def f(x): return pow(2*x,2) # alternate powering notation

 >>> Sigma(f,10,1)
 405328

So we now have a Python definition of sigma that’s consistent with the following, using more traditional typography:

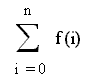
We’re free to define our f however we like, and pass it to Sigma( ) as a parameter, i.e. Sigma(f,n).

THE ADVANTAGE OF IMMEDIATE FEEDBACK

Now, in the above interactive session with Python, were we somehow criss-crossing between two separate disciplines, math and computer programming? I suppose you could say so. But from my point of view, the VHLL is acting very much like a math notation, with the added advantage that it’s interactive and therefore gives instantaneous feedback. You don’t have to wait for the teacher to correct your homework to know whether you’re doing the syntax properly, getting the concepts.

Plus I think you’ve done something which more traditional K-12 text books have a hard time communicating: by writing both sigma and f as functions, and passing f to sigma as a parameter, you’re better helping students form the generic concept of an ‘operator’-- operators which work on other operators.

CASE STUDY: PI NOTATION

Last note: It really makes sense, while you’re developing a notion of Sigma, to develop the corresponding notion of Pi (capital greek letter). Sigma is to Pi as addition is to multiplication.

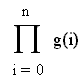
Note that lowercase pi is the ratio of the circumference of a circle to its diameter -- but here we're using uppercase Pi). In naming our functions (below) we’re taking advantage of Python’s case sensitivity and capitalizing both Sigma and Pi to help make the hyperlink to the capital greek letter equivalents.

 >>> def Sigma(f,s,n):
        return reduce(add,[f(x) for x in  range(s,n+1)])

 >>> def Pi(f,s,n):
        return reduce(mul,[f(x) for x in range(s,n+1)])

So now you want to product of the first 20 prime numbers?

Well, we need a function that outputs the ith prime. I’m going to simply import something I wrote and saved earlier for that purpose:

 >>> import primes
 >>> def getprime(i):
         """
         Return last term from first i primes in sequence
         """
         return primes.get2nb(i+1)[-1]

 >>> getprime(0) # 0th prime is 1st  in the list
 2
 >>> getprime(1) # and so on...
 3
 >>> getprime(2)
 5
 >>> map(getprime,range(20))
 [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 
 59, 61, 67, 71]
 >>> Pi(getprime,0,5) # range(5) = [0,1,2,3,4]; 2 is 0th prime
 30030

That’s 2 * 3 * 5 * 7 * 11 * 13 -- builds up quickly, so if you plan to go a lot higher you’ll want your getprime() to output "long integers". Something to discuss in another lesson, e.g. when we start generating primes of 100 digits or more:

 >>> primes.bigppr()
 Working...
 Percent chance of being prime: 99.9999999999
 Elapsed time: 4.75655894333 seconds
 372106324940930886970978581418419848613328680550192
 99361491901238607299599499654601573369854695139659L

The L on the end means "long integer"-- calculators usually can’t get into this territory at all, but in the math classroom of the future, students will as a matter of routine (or so I would hope).

TOPICS FOR FURTHER EXPLORATION

Because of the alternate meaning of + (add) with regard to strings, we can limber up student minds a little by using our sigma function a little differently:

 >>> def wordscan(i): return 'TYGRE'[i]

 >>> Sigma(wordscan,0,4)
 ‘TYGRE’

This may seem like a trivial "programming trick" and not very "math oriented" but this is not the case. What’s true about algebra systems is that whereas we might use the symbols + and * for operations, we don’t prejudice ourselves regarding (a) what these might mean or (b) what kind of object they might operate upon.

For example, in group theory, we define an operator and a set of objects such that various rules are followed e.g. there’s an identity object such that:

object.op(identity) --> object

and an inverse object.inv() for every object such that:

object.op(object.inv()) --> identity

Note that I’m using object oriented notation to express math concepts here. It works, plus reinforces the syntax of the Python language -- and most other OO languages as well. For a discussion of OO notation with regard to math concepts, see my OOP Meets Algebra, Suggesting New "Ways of Looking.

Because Python lets you override the meaning of + and * when defining objects (as well as other operators), we’re in an ideal environment in which to explore Sigma with respect to different meanings of + (as in the case of ‘TYGRE’ above).

To take another example, consider vectors as objects under consideration and define a function that returns a random vector with integer coordinates between -10 and 10:

 >>> import random, coords # coords.py is an OCN module 
 >>> def randomvector(i):
        x = random.randint(-10,10) 
        y = random.randint(-10,10) 
        z = random.randint(-10,10) 
        return coords.Vector((x,y,z))
 >>> randomvector(1)
 Vector (2.0, 3.0, -5.0)
 >>> randomvector(1)
 Vector (7.0, 4.0, 0.0)

So now we can apply sigma to a list of random vectors, without changing the code in any way, and get a vector result:

 >>> Sigma(randomvector,0,10)
 Vector (-23.0, 19.0, 18.0)

Even though sigma is defined around the concept of ‘add’ (uses the ‘add’ operator), the meaning of ‘add’ is specific to the algebra at hand. In a vector algebra + means we add the vectors to return a vector.

We can talk about the "closure" property here—another characteristic of groups is that ops with objects always get you more objects of the same type.

CONCLUSIONS

I hope I’ve showed in this paper that a Pythonic approach may stimulate thinking at a higher level of abstraction than is normally achieved in K-12 today, in part because of:

the "operator override" feature (making + or * mean different things)
the "operating on operators" feature (passing functions to other functions)
the interactive, immediate feedback environment in general, which frees the student to concentrate on the problem even while relying on tools previously programmed and/or introduced in earlier lessons.

This is an exciting world we could be entering. I would think professional educators would be chomping at the bit to make this world a reality for more students.

Certainly many students are anxious to learn how to use their computers, which are becoming ever more powerful, affordable and ubiquitous. The mathematics classroom is a logical place to see to it that this real student need is addressed, and in a way consistent with the larger goals of an intelligently designed, high quality math curriculum.

For further reading:

Python resources at this website
Trends in Early Math Education
Symbols and Operations
Sigma and Sphere Packing (math-teach, Jan 2001)
Computers vs. Calculators: A Case Study (math-learn, Feb 5, 2001)
Euclid's Algorithm and Euler's Totient Function (math-learn, Feb 24, 2001)
Using a VHLL to explore crypto & group theory (Four parts, Mar 2001)

CP4E 4D

Oregon Curriculum Network